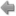Παράρτημα B: Συνθήκη αμεταθετότητας συστήματος τοιχωμάτων
|
1. Ασύμμετρο σύστημα
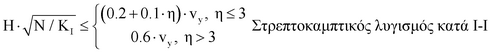
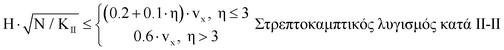
όπου: I, II είναι οι κύριοι άξονες ελαστικότητας τοιχωμάτων.
2. Συμμετρικό ως προς δύο άξονες σύστημα
Ι-Ι: Τίθεται vy=1 .............Μεταφορικός λυγισμός
ΙΙ-ΙΙ: Τίθεται vx=1 ...........Μεταφορικός λυγισμός
III-III:
![]()
3. Υπολογισμός των συντελεστών vx και vy συστήματος τοιχωμάτων
Στη γενική περίπτωση τυχόντος συστήματος τοιχωμάτων τα διαδοχικά βήματα υπολογισμού είναι τα ακόλουθα:
3.1. Μητρώο δυσκαμψίας
Κάθε κατακόρυφο στοιχείο (i) χαρακτηρίζεται από το κέντρο βάρους Gi, από το ελαστικό κέντρο Ki και από τους κύριους άξονες αδράνειας (ξi, ηi) της διατομής του. Οι ροπές αδράνειας ως προς τους άξονες αυτούς και η στρεβλωτική αδράνεια ως προς το σημείο Ki γράφονται αντίστοιχα Iξi, Iηί και Iκί. Στο τυχόν γενικό σύστημα αναφοράς Oxyz το μητρώο δυσκαμψίας του συστήματος γράφεται (Σχήμα. Β.1):
όπου:
![]()
![]()
![]()
![]()
![]()
![]()
Ε = μέτρο ελαστικότητας σκυροδέματος.
3.2. Ελαστικό κέντρο - κύριοι άξονες
Οι συντεταγμένες του ελαστικού κέντρου Κ του συστήματος δίδονται από τις σχέσεις:
![]()
και ο προσανατολισμός των κύριων αξόνων ελαστικότητας (I, II) καθορίζεται από την γωνία ωκ της σχέσης (Σχήμα Β.1):
![]()
Η οξεία γωνία ωκ που προκύπτει από την παραπάνω σχέση (θετική ή αρνητική) καθορίζει την θέση του άξονα I αν Kxx > Kyy ή του άξονα II αν Kxx < Kyy. Στο σύστημα αναφοράς των κύριων αξόνων ελαστικότητας (I,II,III) θα έχουμε τις μεταφορικές δυσκαμψίες του συστήματος:
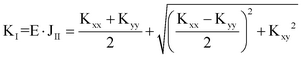
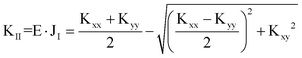
και την στρεβλωτική δυσκαμψία:
![]()
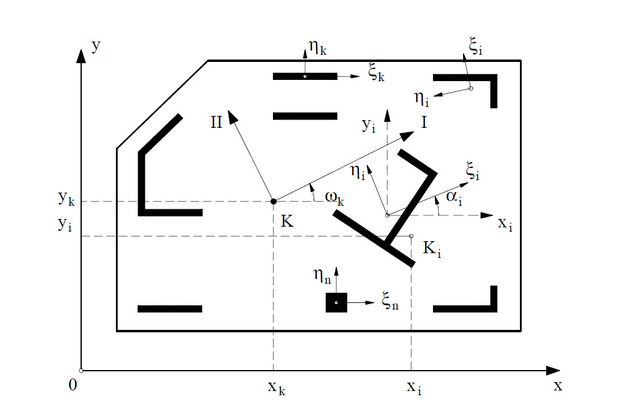
Σχήμα Β.1: Σύστημα τοιχωμάτων.
3.3. Παράλληλη διάταξη στοιχείων
Στην ειδική περίπτωση κατακόρυφων στοιχείων με παράλληλη διάταξη των κύριων αξόνων αδράνειας (ξi, ηi) θα έχουμε Kxy = Kyx = 0 και:
![]()
![]()
![]()
![]()
![]()
Οι κύριοι άξονες (I, II) θα έχουν τον ίδιο προσανατολισμό με τους άξονες (ξi, ηi) και οι συντεταγμένες του ελαστικού κέντρου Κ θα είναι:
![]()
Οι κύριες δυσκαμψίες του συστήματος δίδονται από τις σχέσεις:
![]()
![]()
![]()
3.4. Τιμές των συντελεστών vx και vy
θεωρούμε το σύστημα αναφοράς Bxyz με αρχή Β το κέντρο των αξονικών δυνάμεων Ni όλων των κατακόρυφων στοιχείων στη βάση τους και άξονες (x, y) παράλληλους προς τους κύριους άξονες ελαστικότητας (I, II) (Σχήμα Β.2). Αν είναι ex και ey οι εκκεντρότητες του ελαστικού κέντρου Κ ως προς το παραπάνω σύστημα αναφοράς, οι αδιάστατοι συντελεστές vx και vy υπολογίζονται από τις σχέσεις:
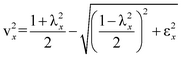
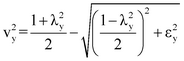
όπου:
![]()
![]()
![]()
![]()
![]()
rb = ακτίνα εκτροπής και ri οι αποστάσεις των αξονικών δυνάμεων Ni από το κέντρο Β, (![]() ).
).
Για λx ≤ 1 ή λy ≤ 1 η θεμελιώδης ιδιομορφή λυγισμού του συστήματος θα έχει δεσπόζοντα στρεπτικό χαρακτήρα, ενώ για λx > 1 και λy > 1 θα έχει δεσπόζοντα μεταφορικό χαρακτήρα (στρεπτοκαμπτικός λυγισμός).
Τέλος, για e = 0 θα έχουμε ν2 = λ2 αν λ2 < 1 ή ν2 = 1 αν λ2 > 1.
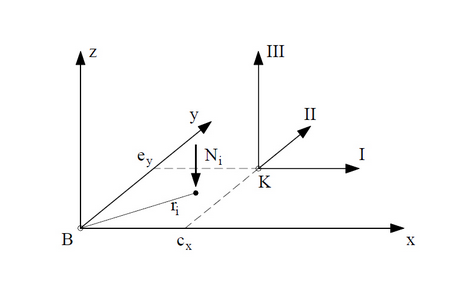
Σχήμα Β.2: Κεντροβαρικό σύστημα αναφοράς